Basic Usage

This is an interactive 3D simulation. To change the view, place your mouse in the view area, and hold and "drag" the mouse to rotate the image. The mouse wheel or a drag on your trackpad should zoom you in or out.

A mathematical investigation of the Tetrahelix and Boerdijk-Coxeter helix, which provides a new formulaic way of producing a continuum of untwisted tetrahelices.

All of the code on this site is released under the GNU General Public License, and I hope you will reuse it.

Creating Objects

You can make this page render a wide variety of 3D objects. Pressing the "circle", "sine", "spiral", "cone" or "helix" buttons will render those objects based on an algorithm for following parametric curves.

To create a new parametric curve at present, you would have to hack the code of this page, which we encourage you to do.

Generated Objects

By enterring in the text area a short snippet of JavaScript defining an anonymous function which takes an integer and returns either -1, 0, 1, or 2, you can produce an unlimited number of shapes. Just enter such javascript and hig the "GO!" button. -1 means "stop." 0, 1 and 2 desrcibe the face to which to add the new tetrahedron.

Perhaps the simplest recipe is a purely periodic generator. An example is:

(i) => { return i<20 ? [ 2,1,0,1,2][i%5]: -1; }

Which simply cycles through an array of 5 values. You can change the numbers (always keeping them 0,1, or 2---go ahead ant try it.

This is a flattened view of a tetrahedron in the 3D generator, as viewed from the outside.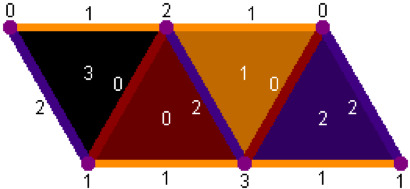

The base (face 3) of each tetrahedron is placed against a face of the previous tetrahedron, as determined by a generator.
Edge 1 of the base of the new tetrahedron is matched against an edge 1 of the previous. Depending on which face it’s placed against, this may be an edge along the base (faces 1 and 3), or one adjacent to the apex (faces 0 and 2).
Edge 0 of each tetrahedron is matched up with edge 2 of the tetrahedron it is placed against.
For a chain of direction 1, no matter what the edge lengths are, the entire chain shares a single edge 1 along the base. This causes tight turns in the resulting constructions.

A Menagerie of Generated Objects

Try using these generators to get interesting shapes.

Giant Square Container

-- found by Nathan (i) => { return i<500 ? (( (i % 22) == 21) || ((i % 22) == 20) ? 1 : 2 ): -1; }

Gentle Helix With Cavity

(i) => { return i<200 ? [ 1,0,0,1,0][i%5]: -1; } 

The LENGTH CLASS

This is an class of objects created by varying the constant K. (i) => { const K = 24; return i<500 ? (( (i % K) == 7) || ((K % 24) == 8) ? 1 : 2 ): -1; }

THIS IS A CLOSE APPROXIMATION TO A TORUS:

(i) => { const K = 4; return i<25 ? (((i % K) == K-1) ? 1 : 2 ): -1; }

THIS IS A VERY NICE APPROXIMATION TO A HELIX WITH A TIGHT CAVITY

(i) => { const K = 9; return i<250 ? (((i % K) == K-1) ? 1 : 2 ): -1; }

THIS IS LIKE K = 9 BUT SIGNIFICANTLY MORE OPEN

(i) => { const K = 10; return i<250 ? (((i % K) == K-1) ? 1 : 2 ): -1; }

FROM K = 9 to K = 18 you produce helixes of various torsion more or less smoothly.

THIS PRODUCES A NICE BROADLY OPEN HELIX

(i) => { const K = 18; return i<250 ? (((i % K) == K-1) ? 1 : 2 ): -1; }

THIS ALSO PRODUCES A NICE BROADLY OPEN HELIX, EVENLARGER

(i) => { const K = 27; return i<250 ? (((i % K) == K-1) ? 1 : 2 ): -1; }

Two very nearly planar structures

“Nearly Flat Sawtooth”

(i) => { const K = 30; return i<250 ? (((i % K) == K-1) ? 1 : 2 ): -1; } (i) => { const K = 41; return i<250 ? (((i % K) == K-1) ? 1 : 2 ): -1; }

A means of Generating Toruses

To generate perfect toruses, you have to check the "Alternate a/b" checkbox, and enter some specific lengths (creating irregular or scalene tetrahedra.) (i) => { const K = 4; return i<24 ? (((i % K) == 0) ? 1 : 2 ): -1; }

Alternate a/b = true; 2b = .95

These numbers (put into the same was as above for 2b, produce different polygonal toriods.)

Triangle: 0.29

Square: 0.648

Pentagon: 0.835

Hexagon: 0.95

Setting 2b to 1.414 produces a straight "beam" different than the Equitetrabeam.

In fact, this method is a basic mechanism for producing toroidal forms are any lengh, which is very useful.

Equitetrabream

This formula with no alternations produces the famous Boerdijk-Coxeter tetrahelix: (i) => { return i<24 ? 2: -1; }

Modify edge lengths thusly produces a square "box beam":

This setting produces the perfectly triangular "Equitetrabeam"

0b = 2a = 1.1547 (2/sqrt(3)

The Funny Square-side Helix

(i) => { const K = 4; return i<100 ? (((i % K) == 0) ? 1 : 2 ): -1; }

This setting produces a funny "sqare-hole helix" whose central cavity is square: 2a = 0b = 1.1547, alternate ab = true

This produces a similar "octagonal helix": 1a = 1b = 1.1547, alternate ab = true